El análisis de funciones es una parte importante de la matemática que se encarga de estudiar el comportamiento de las funciones. Cómo crecen o decrecen, donde alcanzan sus valores máximos o mínimos, si presentan cortes o asíntotas, los valores que toman en x o en y, etc. Este tipo de estudio no solo permite comprender mejor las propiedades de una función, sino también predecir su comportamiento y resolver problemas donde no se conocen datos sobre una función.

El dominio de una función es el conjunto de valores en x para los cuales la función está definida. Por ejemplo, una función que solo pasa por encima del eje de las abscisas (eje x) no va a estar definida para valores negativos de x. Encontrar el dominio es el primer paso para analizar una función correctamente. Una función que se extiende por valores tan grandes que son considerados infinitos, tiene un dominio que se escribe como Dom=(- ∞ ; ∞ ) o R-{x} si se excluye algún valor. La imagen es el conjunto de valores en y que la función puede tomar. A veces se puede deducir directamente, pero en muchos casos se analiza mirando el gráfico o sacando el dominio de la función inversa (cambiar de lugar a x e y y despejar hasta dejar a y en un termino separado), debido a que su dominio es igual a la imagen de la función original. Por ejemplo, una función que se extiende hacia el infinito en ambos sentidos verticalmente tiene una imágen representada como Img=(- ∞ ; ∞ ) o R-{x} si se excluye algún valor.

Las raíces de una función son los valores de x donde y=0, es decir, por donde la función corta al eje de las abscisas. Se pueden encontrar analíticamente con la fórmula f(x)=0 u observando el grafico. La ordenada al orígen es el punto en el que x=0, es decir, el punto en el que la función pasa por el eje de las ordenadas (eje vertical). Analíticamente se puede calcular reemplazando el valor en x con 0, osea f(0). También se puede encontrar observando el gráfico.

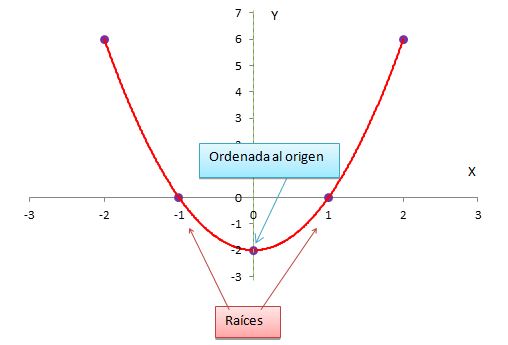
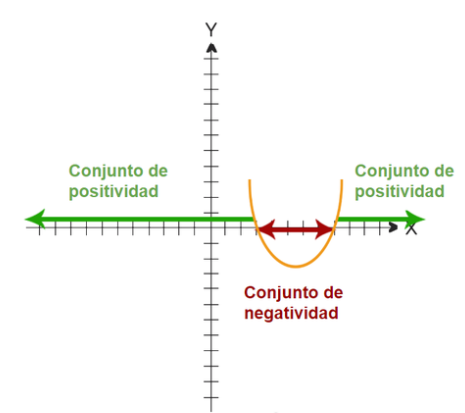
Tomando en cuenta el eje de las abscisas y la función, podemos denominar el conjunto de positividad y negatividad de la función, es decir, las partes que se encuentran sobre o abajo del eje de las abscisas. El conjunto de positividad está conformado por todos los valores de x que resulten en un valor de y mayor a 0. El eje de negatividad se conforma de todos los valores de x que resulten en un valor de y menor a 0. Se representan como una unión de puntos, por ejemplo (0;3)u(5;7).

Las funciones tienen una propiedad llamada paridad, que se refiere a la simetría en relación al eje de las ordenadas. Una función par es aquella que mantiene igual si el valor x pasa a aser su opuesto, es decir, f(-x)=f(x). Esto significa que los dos lados de la función son un reflejo del otro. Imaginando que podemos doblar el gráfico a la mitad usando el eje y como parte media, ambos lados quedarían en la misma posición. Las funciones consideradas impares son las que al invertir el valor de x resultan en f(-x)=-f(x), lo que significa que para lograr superponer los dos lados de la función va a haber que doblar el gráfico primero usando el eje de las ordenadas como punto medio, y luego el eje de las abscisas. También existen las funciones que no son consideradas pares ni impares debido a que no cumplen ninguna de las dos condiciones.

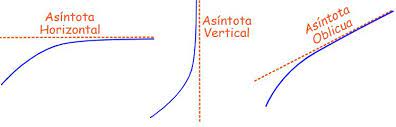
Las asíntotas son líneas que se extienden hasta el infinito al que la función se aproxima, pero nunca llega a tocar. Existen tres tipos principales: verticales, horizontales y oblicuas. Las asíntotas solo pueden aparecer en funciones racionales, irracionales, exponenciales y logarítmicas debido a que por cómo están formadas. Estas funciones no pueden incluir algunos valores de x porque causarían un error. Las asíntotas verticales ocurren cuando la función se dispara hacia el infinito cerca de ciertos valores de x donde no está definida, como en divisiones por cero. Las asíntotas horizontales, al igual que las verticales, son líneas que se extienden hacia el infinito en ambos lados, en este caso de manera horizontal, a las que la función se les acerca pero nunca las llega a tocar. Por último, las asíntotas oblicuas aparecen cuando la función crece indefinidamente siguiendo una línea con pendiente, esto sucede en algunas funciones donde el grado del numerador es uno mayor que el del denominador. Este tipo de asíntota no se representa como una línea, sino que es una función lineal propia, es decir, se expresa como f(x)=mx+b.